
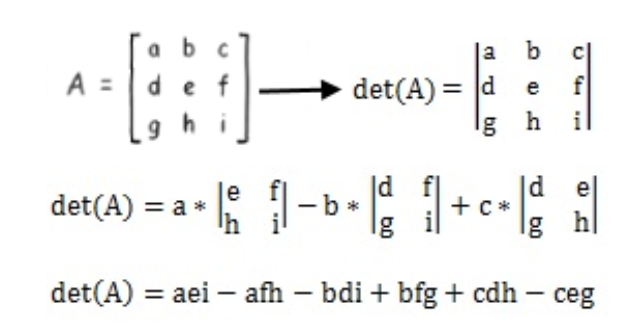
For any square matrix A, the determinant of A is denoted by det A (or) |A|. The determinant of matrix is defined only for square matrices. The determinant D of the given matrix is D = 8.Ī) row (1) is multiplied by 2 and row (3) by - 3, hence according to property (3) above, the determinant is 2 (-3) D = - 6 D.The determinant of matrix is the sum of products of the elements of any row or column and their corresponding co-factors. The matrix is now in triangular form and its determinant is given by the product of the entries in the main diagonal.ĭeterminant of the triangular matrix = (1)(-1)(4)(2)(1) = - 8 = - D Step 5: add a multiple of a row to another row the determinant does not change: - D. Step 4: add multiples of rows to other rows the determinant does not change: - D. Step 3: add a multiple of a row to another row the determinant does not change: - D. Step 2: add multiples of rows to other rows the determinant does not change: - D. Step 1: Exchange row 4 and 5 according to property (2) the determinant change sign to: - D. Let D be the determinant of the given matrix A. The determinant of matrix \( A = \beginįind the determiant, in terms of D, of the following matrices
Use the method of row echelon form to calculate the determinant of the matrices. Questions on Determinant and Row Reduction Part 1 The matrix is now in triangular form and its determinant is given by the product of the entries in the main diagonalĭeterminant of the triangular matrix = (-1)(2)(1)(8) = - 16 = -(- D) = D = Det(A) Step 3: interchange rows (2) and (3) and according to property (2) the sign of the determinant change sign to -(- D) Step 2: interchange rows (3) and (4) and according to property (2) the sign of the determinant change sign to - D Step 1: subtract row (1) from row (3) and according to property (1) the determinant does not change. Note: Compare this method of calculating the determinant of a square matrix with the method of cofactors in determinant of a square matrix. The matrix is now in triangular for and its determinant is given by the product of the entries in the main diagonalĭeterminant of the triangular matrix = (-1)(1)(-7)(2)(-3/2) = - 21 = D = Det(A) Step 4: we add a multiple of a row to another row as shown below and according to property (1) the determinant does not change D. Step 3: we add a row to another row as shown below and according to property (1) the determinant does not change D. Step 2: we add multiples of rows to other rows as shown below and according to property (1) the determinant does not change D. Step 1: we add rows to other rows as shown below and according to property (1) the determinant does not change D. Now that the matrix is in triangular form, the determinant of the given matrix is calculated as the product of the elements in the main diagonal (upper left to lower right).ĭeterminant of the triangular matrix = (2)(4)(-17) = - 136 = D = Det(A)Ĭombine rows and use the above properties to rewrite the 5 × 5 matrix given below in triangular form and calculate its determinant. Step 3: subtract 2 times row(2) from row(3) - see property (1) above - the determinant does not change D

Step 2: subtract 2 times row(1) from row(3) - see property (1) above - the determinant does not change D Step 1: add row(1) to row(2) - see property (1) above - the determinant does not change D Let D be the determinant of the given matrix.

Property 3: If a row of a given matrix is multiplied by a scalar k, then the determinant of the matrix obtained is equal to the determinant of the original matrix multiplied by k.Įxamples on Finding the Determinant Using Row Reduction Example 1Ĭombine rows and use the above properties to rewrite the 3 × 3 matrix given below in triangular form and calculate it determinant. Property 2: If two rows of a given matrix are interchanged, then the determinant of the matrix obtained is equal to the determinant of the original matrix multiplied by - 1. Property 1: If a linear combination of rows of a given square matrix is added to another row of the same square matrix, then the determinants of the matrix obtained is equal to the determinant of the original matrix. We reduce a given matrix in row echelon form (upper triangular or lower triangular) taking into account the following properties of determinants: The determinant of the given matrix is calculated from the determinant of the triangular one taking into account the properties listed below. The main idea is to row reduce the given matrix to triangular form then calculate its determinant.

DETERMINANT OF A MATRIX HOW TO
Examples and questions with their solutions on how to find the determinant of a square matrix using the row echelon form are presented.


 0 kommentar(er)
0 kommentar(er)
